MCMC 探秘(一)
2019 年 12 月 28 日 | 分类于 学习中最近在看一些跟 MCMC 有关的研究,发现有很多东西是以前在学校里没有接触过的,所以想稍微整理一下,方便自己、也方便读者未来对 MCMC 进行更深入的了解。这里我先立个 Flag,计划写成一个系列,虽然以很大的可能最后会鸽掉。本文是这个系列的第一篇,将引入一个重要的概念,几何遍历性(Geometric ergodicity)。
MCMC 的内容非常广,我们先从一个典型的算法开始,即 Gibbs 抽样(Gibbs sampler)。我们的目的是从一个联合分布 \(p(x,y)\) 抽取 \(X\) 和 \(Y\) 的样本,但通常 \(p(x,y)\) 的形式比较复杂,很难直接抽样。但如果两个条件分布,\(p(x\vert y)\) 和 \(p(y\vert x)\),具有某些特殊的形式,使得从条件分布抽样很简单,那么 Gibbs 抽样就可以派上用场。我们任意指定一个初值 \(X_0\),然后进行下面的迭代:
- 抽样 \(Y_i\sim p(y\vert x=X_i)\)
- 抽样 \(X_{i+1}\sim p(x\vert y=Y_i)\)
那么在一定的条件下,\((X_i,Y_i)\) 的分布会随着迭代次数 \(i\) 的增大而逐渐逼近 \(p(x,y)\)。
为了直观地展示这个过程,我们采用这份文档中的一个例子。首先如下定义 \((X,Y)\) 的联合分布:
\[p(x,y)=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\binom{n}{x}y^{x+a-1}(1-y)^{n-x+b-1}.\]是不是觉得很复杂?没错,我就是故意的,欢迎大家顺着网线来打我。经过一些简(fá)单(wèi)的推导,我们可以发现
\[X|\{Y=y\}\sim Binomial(n,y),\quad Y|\{X=x\}\sim Beta(a+x,b+n-x),\]也就是说两个条件分布都是我们熟悉的分布。于是利用 Gibbs 抽样,我们可以进行如下的迭代:
- 抽样 \(Y_i\sim Beta(a+X_i,b+n-X_i)\)
- 抽样 \(X_{i+1}\sim Binomial(n,Y_i)\)
【思考题:事实上上面的这个例子不需要通过 MCMC 就可以获得 \(X\) 的精确密度函数及抽样方法,请尝试推导之。】
我们固定 \(a=2,b=5,n=30\),然后得到不同步数 \(i\) 下的 \(X\) 样本。
n = 30
a = 2
b = 5
sample_y = function(x, a, b, n) rbeta(length(x), a + x, b + n - x)
sample_x = function(y, a, b, n) rbinom(length(y), size = n, prob = y)
gibbs = function(x0, niter, a, b, n)
{
x = x0
for(i in 1:niter)
{
y = sample_y(x, a, b, n)
x = sample_x(y, a, b, n)
}
list(x = x, y = y)
}
set.seed(123)
x0 = rbinom(10000, size = n, prob = 0.5)
res1 = gibbs(x0, niter = 1, a = a, b = b, n = n)
res10 = gibbs(x0, niter = 10, a = a, b = b, n = n)
res100 = gibbs(x0, niter = 100, a = a, b = b, n = n)
为了考察 Gibbs 抽样的效果,我们利用得到的样本来近似当前步数下的 \(X\) 的密度函数,然后与它的真实值进行比较。以下分别是 \(i=1\),\(i=10\),和 \(i=100\) 时的结果:
library(ggplot2)
pmf_x = function(x, a, b, n)
{
freq_x = table(x)
est_pmf = numeric(n + 1)
names(est_pmf) = as.character(0:n)
est_pmf[names(freq_x)] = freq_x / sum(freq_x)
ind = 0:n
true_pmf = choose(n, ind) * beta(a + ind, b + n - ind) / beta(a, b)
list(ind = ind, true = true_pmf, est = est_pmf)
}
vis_x = function(res, a, b, n)
{
pmf = pmf_x(res$x, a, b, n)
gdat = data.frame(ind = rep(pmf$ind, 2), den = c(pmf$est, pmf$true),
type = rep(c("Gibbs", "True"), each = n + 1))
ggplot(gdat, aes(x = ind, y = den, fill = type)) +
geom_bar(stat = "identity", position = "dodge", alpha = 0.5) +
scale_fill_brewer("Type", type = "qual", palette = "Set1") +
xlab("x") + ylab("Density") +
theme_bw()
}
vis_x(res1, a, b, n)
vis_x(res10, a, b, n)
vis_x(res100, a, b, n)
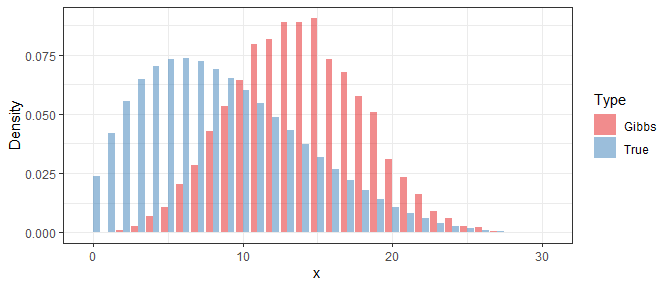
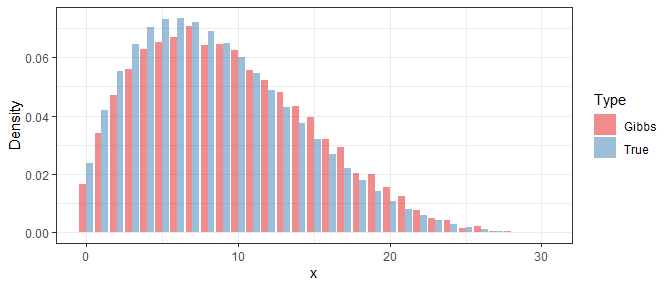
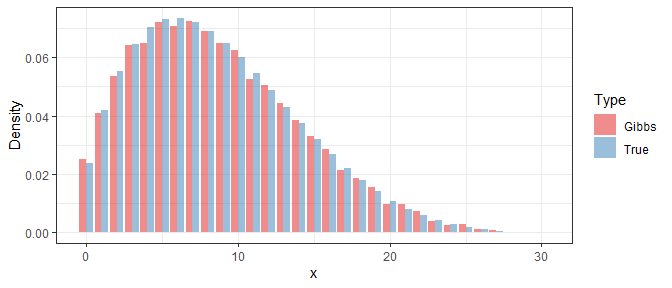
可以看出,即使在最开始 Gibbs 样本与真实分布相差甚远,但经过10步以后它们的差别已经显著减小,而在100步后就几乎没有区别了。
于是我们就迎来了 MCMC 中一个非常重要但又很难回答的问题:迭代多少次才够?
要回答这个问题,我们先定义一个衡量分布之间差异的指标。在这个例子中,\(X\) 的取值范围是 \(0,1,\ldots,n\)。假设真实的密度函数是 \(p(x)\),而根据 Gibbs 抽样迭代 \(k\) 次后所得样本的密度函数是 \(q^{(k)}(x)\),那么我们可以计算
\[d_{TV}(p,q^{(k)})=\frac{1}{2}\sum_{x=0}^n\vert p(x)-q^{(k)}(x)\vert,\]这便是所谓的全变差距离(Total variation distance,简称 TV 距离)。我们略微修改之前的程序,记录下每步迭代后的 \(d_{TV}(p,q^{(k)})\) 取值:
dtv = function(x, a, b, n)
{
pmf = pmf_x(x, a, b, n)
0.5 * sum(abs(pmf$est - pmf$true))
}
gibbs_dtv = function(x0, niter, a, b, n)
{
tv = c()
x = x0
for(i in 1:niter)
{
y = sample_y(x, a, b, n)
x = sample_x(y, a, b, n)
tv = c(tv, dtv(x, a, b, n))
}
tv
}
set.seed(123)
x0 = rbinom(10000, size = n, prob = 0.5)
tv = gibbs_dtv(x0, niter = 100, a = a, b = b, n = n)
qplot(1:100, tv, geom = c("point", "line")) +
xlab("# Gibbs Steps") + ylab("TV Distance") + theme_bw()
qplot(1:100, log10(tv), geom = c("point", "line")) +
xlab("# Gibbs Steps") + ylab("log(TV Distance)") + theme_bw()
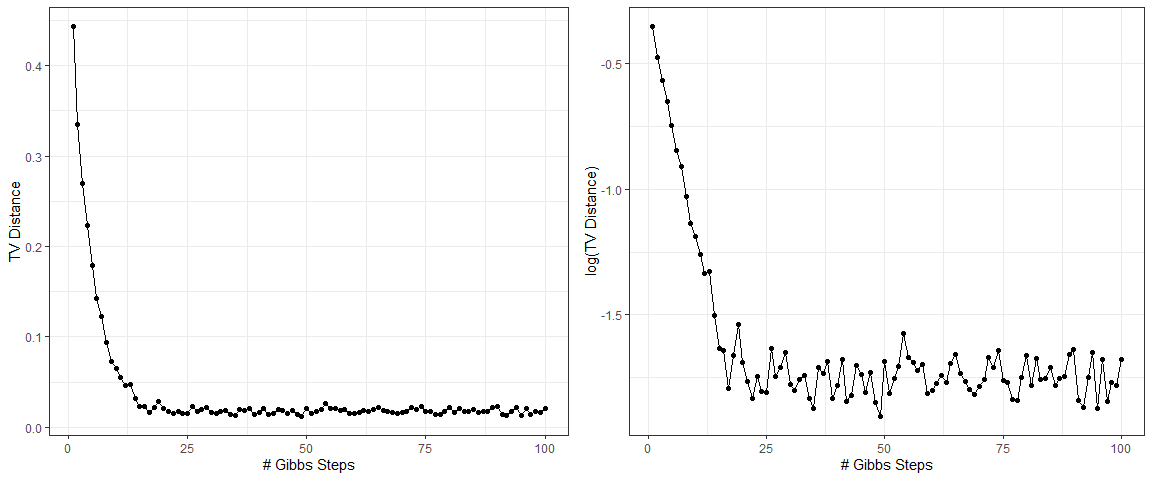
这里左图是 \(d_{TV}(p,q^{(k)})\) 随 \(k\) 的变化,右图是对 \(d_{TV}(p,q^{(k)})\) 取对数后的结果。可以看出,右图的散点在前期基本处在一条直线上,说明 Gibbs 样本与真实分布的 TV 距离几乎是随着迭代步数而指数下降的。后期保持一个接近于零的常数是因为 \(q^{(k)}(x)\) 是用样本的经验分布逼近的,因此会有一些跟样本量有关的随机误差,它不会随着迭代步数的增大而消失。
我们以后会发现,这一误差呈指数衰减的性质会在 MCMC 的分析中占据非常重要的位置。用更正式的语言来说,如果一个 MCMC 算法经过有限步迭代后样本的分布与真实分布之间的 TV 距离(\(d_{TV}(p,q^{(k)})\))随迭代步数(\(k\))呈指数性的衰减,即存在常数 \(C>0\) 和 \(\rho>0\) 使得
\[d_{TV}(p,q^{(k)})\le Ce^{-\rho k},\]那么我们就称这个 MCMC 算法是几何遍历(Geometric ergodic)的。几何遍历性之所以重要,是因为它代表了快速收敛的特点:具有几何遍历性的 MCMC 算法通常只需很少的步数就可以近似真实的分布,正如前面的例子展示的那样。事实上,对于大部分我们使用的 MCMC 算法,几何遍历性都是成立的,但要严格进行证明却不是一件简单事。关于这一点,就放到以后再说了。
欲知后事如何,且听不知道有没有下回的下回分解。
参考文献:Sean Meyn and Richard Tweedie (1993). Markov Chains and Stochastic Stability, Springer.
附:【思考题】答案
经过推导,可以发现
\[Y\sim Beta(a,b),\quad X|\{Y=y\}\sim Binomial(n,y),\]换言之,\(Y\) 服从一个 Beta 分布,取值范围是 \((0,1)\),而给定 \(Y=y\),\(X\) 服从一个概率为 \(y\) 的二项分布。\(X\) 精确的密度函数为
\[p(x)=\binom{n}{x}\frac{B(a+x,b+n-x)}{B(a,b)},\]其中 \(B(a,b)=\Gamma(a)\Gamma(b)/\Gamma(a+b)\) 是 Beta 函数。


